6月の上旬,中西先生の間でこんな会話がありました.
「田中君」
「はい?」
「19日,俺出張があるんで,システム科学概論に出てくれんか」
「はあ!?」
システム科学概論は,中川先生と中西先生が担当されている科目です. 対象はシステム工学部1年生.5学科全員です.必修科目なので, 受講者は300人を越えます. 入学して間もない学生に,システム工学あるいはシステム科学というのが どういうものかを,具体例を挙げて解説していくという内容です.
私はこの科目にはほぼノータッチ. 7月下旬に試験をする際には,大部屋を2つ取って受講者を振り分け, 監督の補助と答案の収集をしました(たしか試験の際も,中西先生は ご出張だったような).
こんな自分に講義をしろと!?
「これを解かしといたらええから(メモを差し出す)」
「(メモを受け取り)はい…」
「通常は,前回の問題を解説してから,今回の問題てことで解いてもらうんやけど」
「前回の問題,ですか?」
「田中にやってもらうときは,解説はええわ.それ板書して,答案を回収してくれたらええよ」
「わかりました…にしても,これは分量が多いですょ.コピーして渡したいんですが」
「うん,そのほうがええかもな」
「ま,TEXで書き直しますゎ」
メモはMacintoshで書かれたものらしく(中西先生はMac党でした. 私は,学生時代にUNIXにどっぷりつかって,今はLinux党になっています), これをTEXで書き直すことにしました.慎重に何度も見直した上で 学生に渡したのですが,書き直したメモに間違いがあり愕然としました.
冒頭のメモの中の間違いというのは, 『結論としてABの長さとBCの長さが等しくなる』の部分で, 正しくは 『結論としてABの長さと``AC''の長さが等しくなる』です. 授業で配布して1分後,学生から指摘を受けて,慌てて訂正部分を板書しました.
「角BAC」は個人的には「∠BAC」と書きたかったし, 「線分BD=線分CD」も単に「BD=CD」のほうが簡潔になるんじゃないかとか, 問の文章の「なぜそうなるのか説明せよ.」というのでは答案が書きにくい だろうなあとか, 文中で気になるところはかなりありました. しかしもう一度読み直して,どうやら 「なぜそうなるのか説明せよ.」の箇所は,名文ではないにしても 深いものを感じました. 学生に出題意図を考えさせるものなんだろう,と. 他の部分も,中西先生なりの意図があるのではと 思うようになり,もらったメモの通りにディジタル化しました. ただし,ACのところをBCと書き間違えたのは,私のミスです.
以下では,「点A」「線分BC」「△ABC」と書くべきところを それぞれ「A」「BC」「ABC」と略記します. 角については省略せず,「角ABC」のように書きます.
授業では,学生からの質問を受け付けました. 「この答案でいいですか?」と持って来るのを見たりもしました. あとで中西先生から聞いたところでは, 質問を聞くのは最小限にしておくべきで, 各学生に一生懸命考えて答案を書いてもらうことがこの授業のやりかた だったそうです.
はじめのうち,何度か耳にした質問は, 6の合同条件のところでした.再掲します:
次に目立った間違いは,証明の内容を丁寧に解説して, 「ゆえにABの長さとACの長さは等しい」で締めくくるもの.
この種の答案は,書いてさっさと出ていった人ばかりです.
おかしいと思わなかったんでしょうね.
この証明が正しいなら,任意の三角形ABCについて,このように D,E,F,Gをとれば,AB=ACとなる. AB≠ACがわかっている三角形ABCでも,AB=ACとなる… という矛盾に気づかなかったんでしょうね.
問は「なぜそうなるのか説明せよ.」ですが, 実際に問われているのは「この証明のおかしいところを説明せよ.」なのです.
「中西先生,とりあえず,TEXにして,図も描いてみました」
「ほな頼むわな」
「この問題,自分なりに考えてみたんですが…」
「うん」
「最初にE,D,F,Gととるところがおかしいんですよね. こんなふうにとれるんですか?」
「結局そこや.存在条件をきちんと検討しとかんと,モノがでけんちゅう例や」
授業をする数日前にこういうやりとりがありました.
この発言の中には特に間違いはありません. ただ,詳細を見ていく際に誤りがあり,それに気づいたのは数か月後になります. その誤りをベースにして,間違ったことを授業中に教えてしまったので, 以下で明らかにして訂正しておきます.
「最初にE,D,F,Gととるところがおかしい」のですが, この直観をもう少し噛み砕いてみましょう.
まず,AB=ACのときにどうなるかを考えてみます. このとき,ABCは二等辺三角形です. そして二等辺三角形の知識を思い出すと, 角BACの二等分線と辺BCの垂直二等分線がぴったり一致することになります. 「交点をE」…というのはとれません.
では,一般の三角形で考えるとどうなるでしょうか? ここで使うのは場合分けです. 答案の最初には「任意に与えられた三角形ABCにおいて, AB=ACとAB≠BCとで場合分けして考える.」と書くわけです.
書き方の問題ですが,「AB=ACとすると…」から書き始めると, 採点者は「なんでそんな仮定を置くねん」と思ってその瞬間に 0点をつけるかもしれません.「採点者」というのはここでは 中西先生のことです.この書き出しの答案が多くてなんかおかしいぞと, 嘆いてらっしゃいました.
場合分けで答案を書く前に,もう一度問題文の1〜8の流れを見ていきます. すると次のことがわかります.
なぜこれが成り立つかは,「証明を追うことで」くらいにしか書けません.
なお,FがABの端にある場合を少し考察しておきます. まずFがAに一致することはありません. FがBに一致する場合, 5までは証明のままで,6からが変わります. 5までのこととFがBに一致することから, CE=BE=FE=GEが言えます. ここで,CとGが一致することを背理法で示します. そうでない,すなわちCとGが異なる点であると仮定すると, △ECGが存在し,これはEC=EGの二等辺三角形になります. しかしGはEからACにおろした足なので,角ECGは直角になります. 底角が直角の二等辺三角形は存在しない(頂角が0度になってしまう!)ので, ECGは存在しません.よってCとGが一致することになります. これと,3で示したAF=AGから, AB=AF=AG=ACとなります. FがABの端にあるかどうかわからないけれどGがACの端にある場合も, これと同様の説明になります.そこで以下, 「AB上」あるいは「AC上」を考える際に両端を除外します.
さて,なぜこれをもってきたかというと,ある程度はひらめきによるものです. しかし中西先生は毎回の演習においてひらめきを否定されていたので (ひらめきとよくいうけど,そういうのは実はステップを踏んでいけば 導き出せるものばかりなんだ,というのをわかってもらうために,毎回 問題を問いてもらっている…そんな趣旨のことを耳にしました), ひらめきを使わないで説明しましょう.
Fの位置は,「線分AB上」か「半直線AB上で,かつ線分AB上ではないところ」 のどちらかになります.(細かいことをいうと,問題文中の 「Eから辺BC,AB,ACにおろした足をそれぞれD,F,Gとする」は 「Dから``直線''BC,AB,ACにおろした足をそれぞれD,F,Gとする」というのが 正しいわけです.とはいえこう書いてしまうと, 必ずしも辺…線分…AB上にFがあるとは限らないことを示唆してしまいます). 前者を「AB上」,後者を「非AB上」と書きます. 一方,Gの位置も同様に,「AC上」か「非AC上」のどちらかになります. 現段階では,Fの位置とGの位置は互いに独立なので, 任意の三角形ABCに対してE,D,F,Gと点をとることができるならば, 次の4つのいずれかちょうどひとつが成り立つことになります.
この4つの場合について,それぞれ証明が8までたどりつくか検討していきましょう. まず,iの場合は,上で述べたように,証明を追えば確かにたどりつき, したがってAB=ACとなります.
次にiiとiiiを飛ばして,先にivを見ます.このとき,7までは問題ありません. そして8のところで和ではなく差をとれば, 「線分AB=線分AF−線分BF=線分AG−線分CG=線分AC」 となりこの式も成立します.
さてiiの場合ですが,7までは問題なく, 8のところが 「線分AB=線分AF+線分BF」と 「線分AC=線分AG−線分CG」 に分かれて,どの線分の長さも正なので結局,AB≠ACとなります. iiiの場合は,8のところが 「線分AB=線分AF−線分BF」と 「線分AC=線分AG+線分CG」 になり,これもまたAB≠ACです.
以上の考察をまとめて答案にすると,次のようになります. 演習の限られた時間内に提出することを想定し,かなりラフな書き方にしています.
任意に与えられた三角形ABCにおいて, AB=ACとAB≠BCとで場合分けして考える.
まずAB=ACの場合は, 角BACの二等分線と辺BCの垂直二等分線がぴったり一致し, 交点がとれない.
次にAB≠ACの場合は, E,D,F,Gがちょうどひとつずつ定まる. ここで,Fと直線AB,およびGと直線ACの位置関係は次の4つの場合で尽くされる.
それぞれの場合について検討する.
iの場合: 証明は8まで成立する. しかしこれはAB≠ACに反する. これは,FおよびGが,このような位置関係になることがないことを意味する.
iiの場合: 証明は7まで成立するが, 8において AB=AF+BF, AC=AG−CGとなる. ゆえにAB≠ACとなり,問題ない.
iiiの場合: 証明は7まで成立するが, 8において AB=AF−BF, AC=AG+CGとなる. ゆえにAB≠ACとなり,問題ない.
iv場合: 証明は7まで成立するが, 8において AB=AF−BF=AG−CG=ACとなる. しかしこれはAB≠ACに反する. これは,FおよびGが,このような位置関係になることがないことを意味する.
この答案では,すでに述べたようにFがAあるいはCと一致する場合については 省略しています. また,AB=ACの場合,一致する2直線から任意の点を選んでEとすると, AB≠ACの中で考察しているi〜ivの場合のうちiとivが成立しiiと iiiが成立しないことも言えますが,問われていることではないので これも省略しています.
この答案を書くときに細心の注意を払わないといけないのは, AB≠ABと勝手に仮定を置いたのではないということです. 「任意の三角形ABCを考えると,AB=ACかAB≠ACのどちらかになる. AB=ACであればかくかく,AB≠ACであればしかじか」と 場合分けをしているのを明示しないといけません. そしてこれを最初に書いておくことで,iの場合でAB≠ACとAB=ACが同時に 成立する原因が,AB≠ACと仮定したことではなく, 「Fが辺AB上にあり,GがAC上にある」と仮定したことにあると言えるわけです.
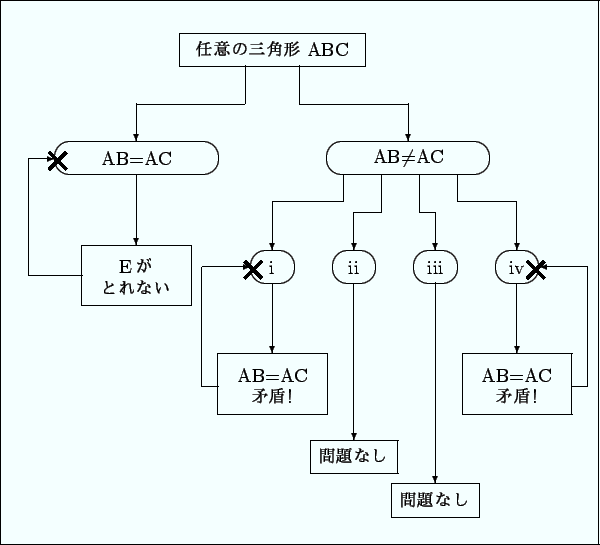
答案の骨格を図にしました. ×印は,矛盾を起こすことになった原因を表します.

ここで,授業を振り返り,懺悔します.
答案が正しいか見てほしいという学生の何人かに対して,
というのも, 「EをABCの内部にとることができれば,FとGをそれぞれAB上とBC上に とることができ」るというのが実は自明でないためです. 下のような三角形ABCを考えると,EはABCの内部にありますが, Fは非AB上に,GはBC上にとることになります.
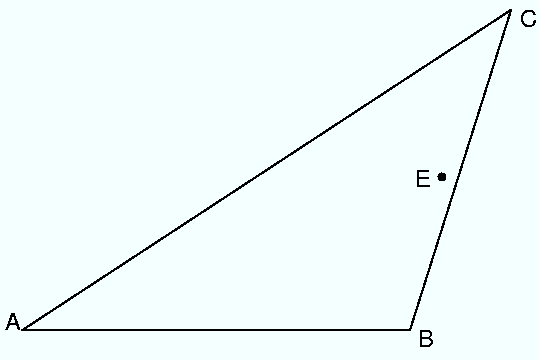
このような位置関係のE,F,Gが存在するかを考察してみたい気にもなりますが (計算力のある人は試してください.私は挫折しました)… 答案を書く際に考慮する必要がありませんでした.Eを落として, FとABとの位置関係,GとACとの位置関係にのみ着目すれば十分でした. EがABCの内部にあるか外部にあるか周上にあるかは, 問題となっている証明の是非と関係がないということです.